Bar plot of the relative gene expression ($\Delta C_T$ method) from the qpcrANOVARE output of a a three-factorial experiment data

Bar plot of the relative expression ($\Delta C_T$ method) of a gene along with the confidence interval and significance

threeFACTORplot(
  res,
  arrangement = c(1, 2, 3),
  bar.width = 0.5,
  fill = "Reds",
  xlab = "none",
  ylab = "Relative Expression",
  errorbar,
  y.axis.adjust = 0.5,
  y.axis.by = 2,
  letter.position.adjust = 0.3,
  legend.title = "Legend Title",
  legend.position = c(0.4, 0.8),
  fontsize = 12,
  fontsizePvalue = 5,
  show.letters = TRUE,
  axis.text.x.angle = 0,
  axis.text.x.hjust = 0.5
)

Arguments

res: the FC data frame created by qpcrANOVARE(x)$Result function on a three factorial data such as data_3factor example data frame.
arrangement: order based on the columns in the output table (e.g. c(2,3,1) or c(1,3,2)) affecting factor arrangement of the output graph.
bar.width: a positive number determining bar width.
fill: a color vector specifying the fill color for the columns of the bar plot. One of the palettes in display.brewer.all (e.g. "Reds" or "Blues", ...) can be applied.
xlab: the title of the x axis
ylab: the title of the y axis
errorbar: Type of error bar, can be se or ci.
y.axis.adjust: a negative or positive number for reducing or increasing the length of the y axis.
y.axis.by: determines y axis step length
letter.position.adjust: adjust the distance between the grouping letters to the error bars
legend.title: legend title
legend.position: a two digit vector specifying the legend position.
fontsize: all fonts size of the plot
fontsizePvalue: font size of the pvalue labels
show.letters: a logical variable. If TRUE, mean grouping letters are added to the bars.
axis.text.x.angle: angle of x axis text
axis.text.x.hjust: horizontal justification of x axis text

Value

Bar plot of the average fold change for target genes along with the standard error or 95% confidence interval as error bars.

Details

The threeFACTORplot function generates the bar plot of the average fold change for target genes along with the significance, standard error (se) and the 95% confidence interval (ci).

Author

Ghader Mirzaghaderi

Examples


#' # See a sample data frame
data_3factor
#>    Type Conc SA Replicate EPO  POCt EGAPDH GAPDHCt
#> 1     R    L A1         1   2 33.30      2   31.53
#> 2     R    L A1         2   2 33.39      2   31.57
#> 3     R    L A1         3   2 33.34      2   31.50
#> 4     R    L A2         1   2 34.01      2   31.48
#> 5     R    L A2         2   2 36.82      2   31.44
#> 6     R    L A2         3   2 35.44      2   31.46
#> 7     R    M A1         1   2 32.73      2   31.30
#> 8     R    M A1         2   2 32.46      2   32.55
#> 9     R    M A1         3   2 32.60      2   31.92
#> 10    R    M A2         1   2 33.37      2   31.19
#> 11    R    M A2         2   2 33.12      2   31.94
#> 12    R    M A2         3   2 33.21      2   31.57
#> 13    R    H A1         1   2 33.48      2   33.30
#> 14    R    H A1         2   2 33.27      2   33.37
#> 15    R    H A1         3   2 33.32      2   33.35
#> 16    R    H A2         1   2 32.53      2   33.47
#> 17    R    H A2         2   2 32.61      2   33.26
#> 18    R    H A2         3   2 32.56      2   33.36
#> 19    S    L A1         1   2 26.85      2   26.94
#> 20    S    L A1         2   2 28.17      2   27.69
#> 21    S    L A1         3   2 27.99      2   27.39
#> 22    S    L A2         1   2 28.71      2   29.45
#> 23    S    L A2         2   2 29.01      2   29.46
#> 24    S    L A2         3   2 28.82      2   29.48
#> 25    S    M A1         1   2 30.41      2   28.70
#> 26    S    M A1         2   2 29.49      2   28.66
#> 27    S    M A1         3   2 29.98      2   28.71
#> 28    S    M A2         1   2 28.91      2   28.09
#> 29    S    M A2         2   2 28.60      2   28.65
#> 30    S    M A2         3   2 28.59      2   28.37
#> 31    S    H A1         1   2 29.03      2   30.61
#> 32    S    H A1         2   2 28.73      2   30.20
#> 33    S    H A1         3   2 28.83      2   30.49
#> 34    S    H A2         1   2 28.29      2   30.84
#> 35    S    H A2         2   2 28.53      2   30.65
#> 36    S    H A2         3   2 28.28      2   30.74

# Before plotting, the result needs to be extracted as below:
res <- qpcrANOVARE(data_3factor, numberOfrefGenes = 1, block = NULL)$Result
#> Analysis of Variance Table
#> 
#> Response: wDCt
#>           Df Sum Sq Mean Sq F value    Pr(>F)    
#> T         11 94.001  8.5456  29.188 3.248e-11 ***
#> Residuals 24  7.027  0.2928                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Relative expression table
#>    Type Conc SA     RE    LCL    UCL     se Lower.se Upper.se  letters
#> 1     S    H A2 5.1934 3.3217 8.1197 0.1309   4.7429   5.6867  a      
#> 2     S    H A1 2.9690 1.8990 4.6420 0.0551   2.8577   3.0846  ab     
#> 3     R    H A2 1.7371 1.1110 2.7159 0.0837   1.6392   1.8409   bc    
#> 4     S    L A2 1.5333 0.9807 2.3973 0.0865   1.4441   1.6280    c    
#> 5     R    H A1 0.9885 0.6323 1.5455 0.0841   0.9325   1.0478    cd   
#> 6     S    L A1 0.7955 0.5088 1.2438 0.2128   0.6864   0.9219     d   
#> 7     S    M A2 0.7955 0.5088 1.2438 0.2571   0.6656   0.9507     d   
#> 8     R    M A1 0.6271 0.4011 0.9804 0.4388   0.4626   0.8500     de  
#> 9     S    M A1 0.4147 0.2652 0.6483 0.2540   0.3478   0.4945      ef 
#> 10    R    M A2 0.3150 0.2015 0.4925 0.2890   0.2578   0.3849       f 
#> 11    R    L A1 0.2852 0.1824 0.4459 0.0208   0.2811   0.2893       f 
#> 12    R    L A2 0.0641 0.0410 0.1002 0.8228   0.0362   0.1134        g
res
#>    Type Conc SA     RE    LCL    UCL     se Lower.se Upper.se  letters
#> 1     S    H A2 5.1934 3.3217 8.1197 0.1309   4.7429   5.6867  a      
#> 2     S    H A1 2.9690 1.8990 4.6420 0.0551   2.8577   3.0846  ab     
#> 3     R    H A2 1.7371 1.1110 2.7159 0.0837   1.6392   1.8409   bc    
#> 4     S    L A2 1.5333 0.9807 2.3973 0.0865   1.4441   1.6280    c    
#> 5     R    H A1 0.9885 0.6323 1.5455 0.0841   0.9325   1.0478    cd   
#> 6     S    L A1 0.7955 0.5088 1.2438 0.2128   0.6864   0.9219     d   
#> 7     S    M A2 0.7955 0.5088 1.2438 0.2571   0.6656   0.9507     d   
#> 8     R    M A1 0.6271 0.4011 0.9804 0.4388   0.4626   0.8500     de  
#> 9     S    M A1 0.4147 0.2652 0.6483 0.2540   0.3478   0.4945      ef 
#> 10    R    M A2 0.3150 0.2015 0.4925 0.2890   0.2578   0.3849       f 
#> 11    R    L A1 0.2852 0.1824 0.4459 0.0208   0.2811   0.2893       f 
#> 12    R    L A2 0.0641 0.0410 0.1002 0.8228   0.0362   0.1134        g

# Arrange the first three colunms of the result table.
# This determines the columns order and shapes the plot output.
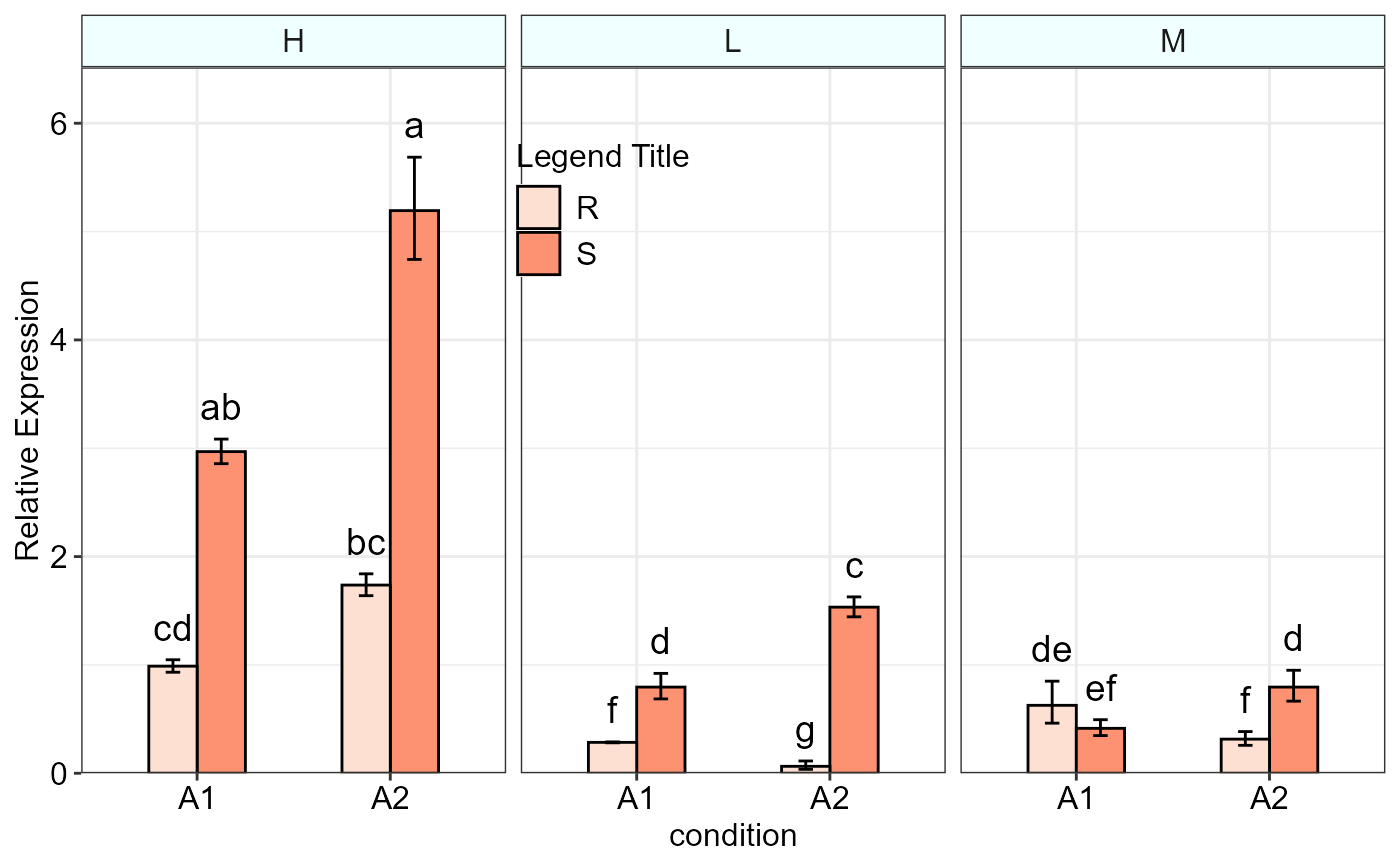
threeFACTORplot(res, arrangement = c(3, 1, 2), errorbar = "se",
    xlab = "condition")



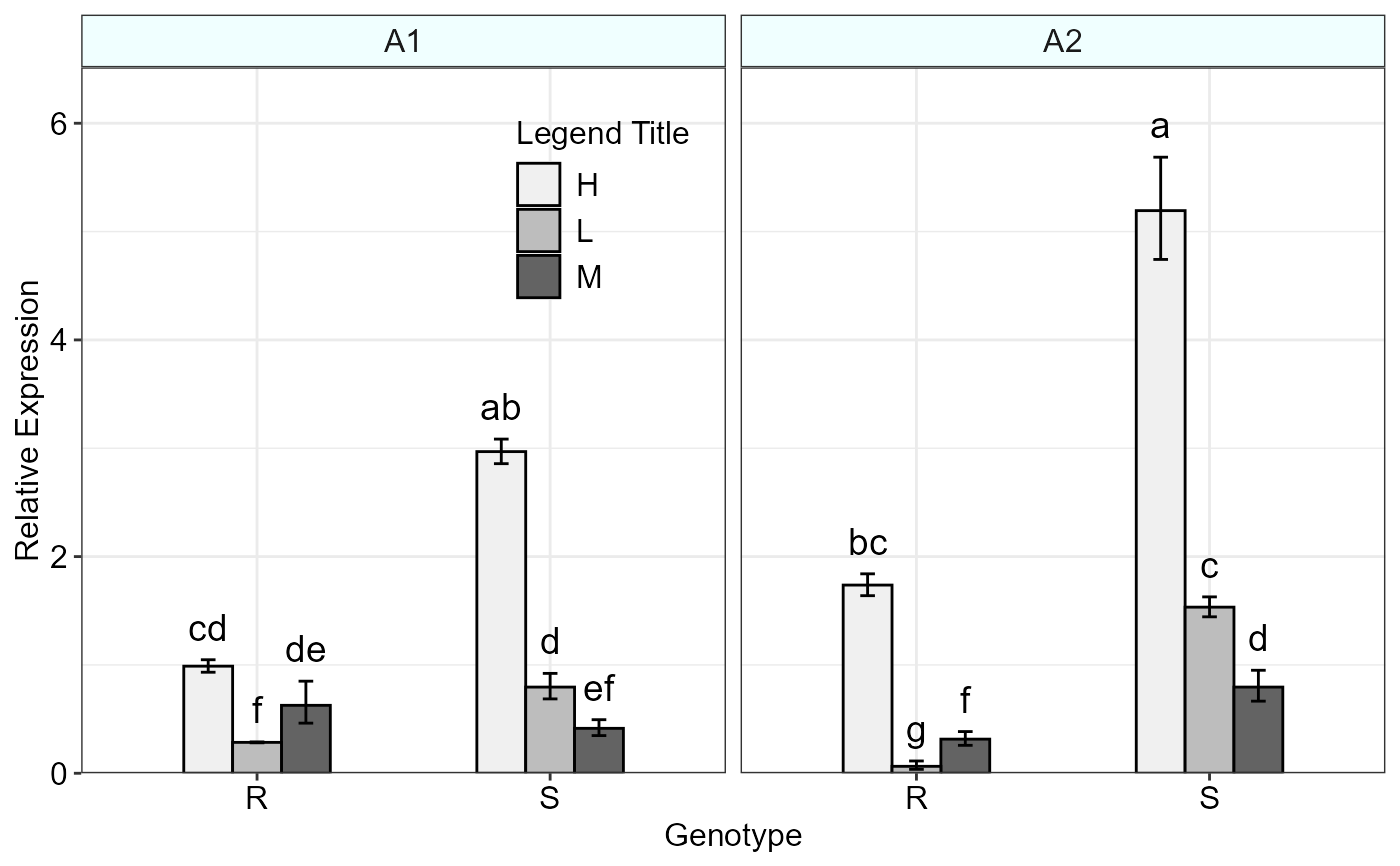
threeFACTORplot(res, arrangement = c(1, 2, 3), bar.width = 0.5, fill = "Greys", 
xlab = "Genotype", ylab = "Relative Expression", errorbar = "se")



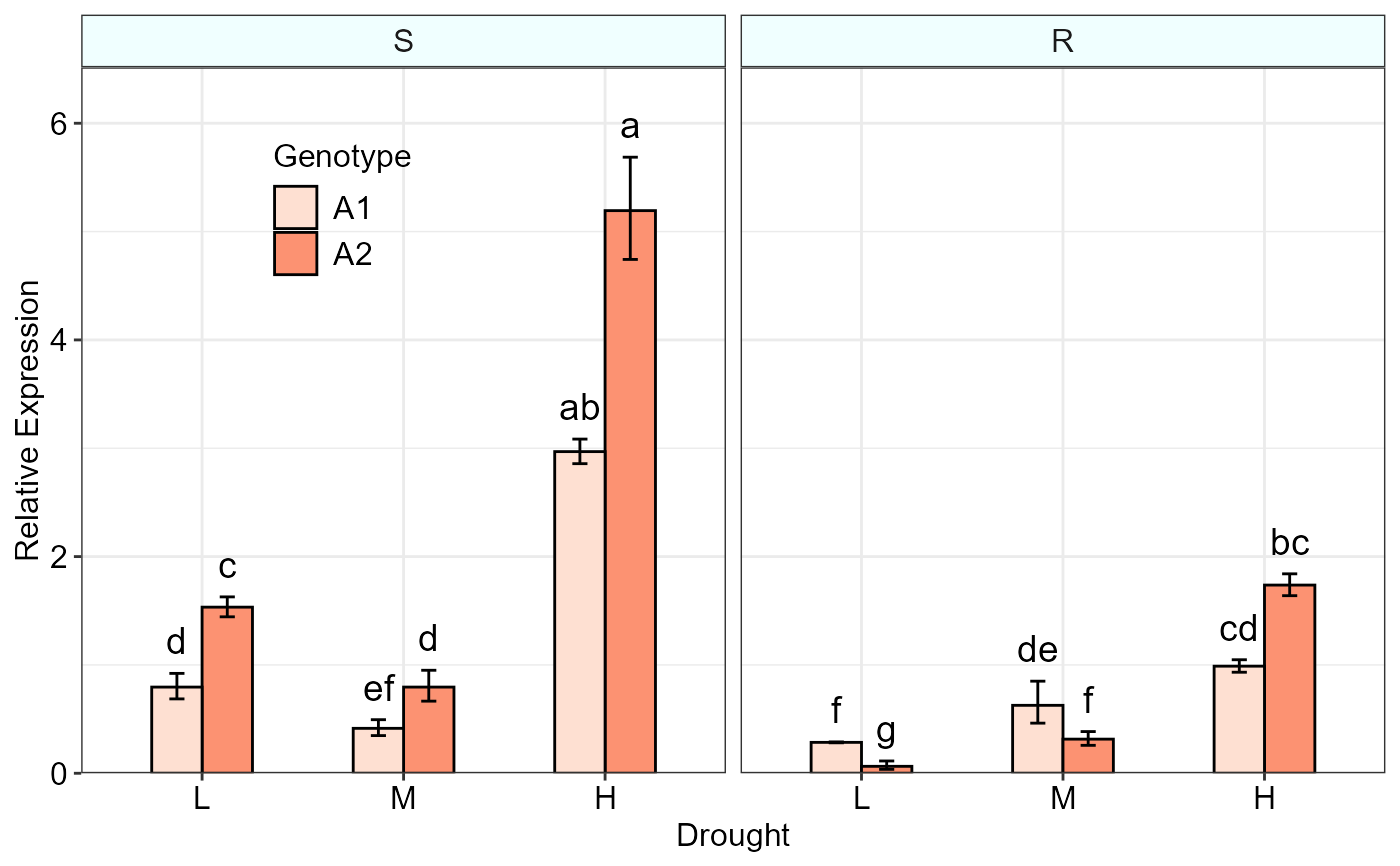
# Reordering factor levels to a desired order.
res$Conc <- factor(res$Conc, levels = c("L","M","H"))
res$Type <- factor(res$Type, levels = c("S","R"))

# Producing the plot
threeFACTORplot(res, arrangement = c(2, 3, 1), bar.width = 0.5, 
fill = "Reds", xlab = "Drought", ylab = "Relative Expression", 
errorbar = "se", legend.title = "Genotype", legend.position = c(0.2, 0.8))



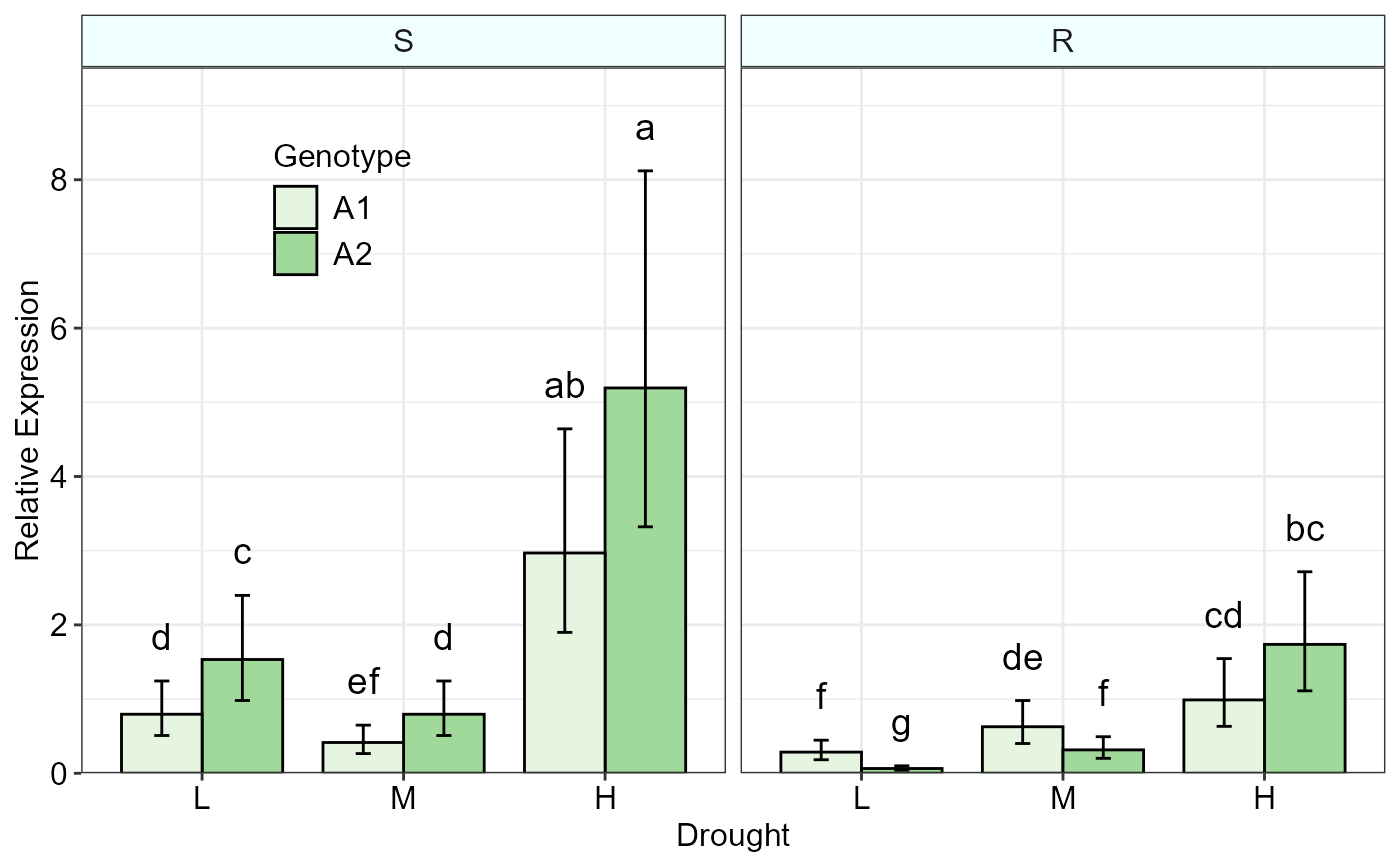
# When using ci as error, increase the 
# y.axis.adjust value to see the plot correctly!
threeFACTORplot(res, arrangement = c(2, 3, 1), bar.width = 0.8, fill = "Greens", 
xlab = "Drought", ylab = "Relative Expression", errorbar = "ci", 
y.axis.adjust = 1, y.axis.by = 2, letter.position.adjust = 0.6, 
legend.title = "Genotype", fontsize = 12, legend.position = c(0.2, 0.8), 
show.letters = TRUE)

Bar plot of the relative gene expression (\(\Delta C_T\) method) from the qpcrANOVARE output of a a three-factorial experiment data

Arguments

Value

Details

Author

Examples

Bar plot of the relative gene expression (\(\Delta C_T\) method) from the `qpcrANOVARE` output of a a three-factorial experiment data